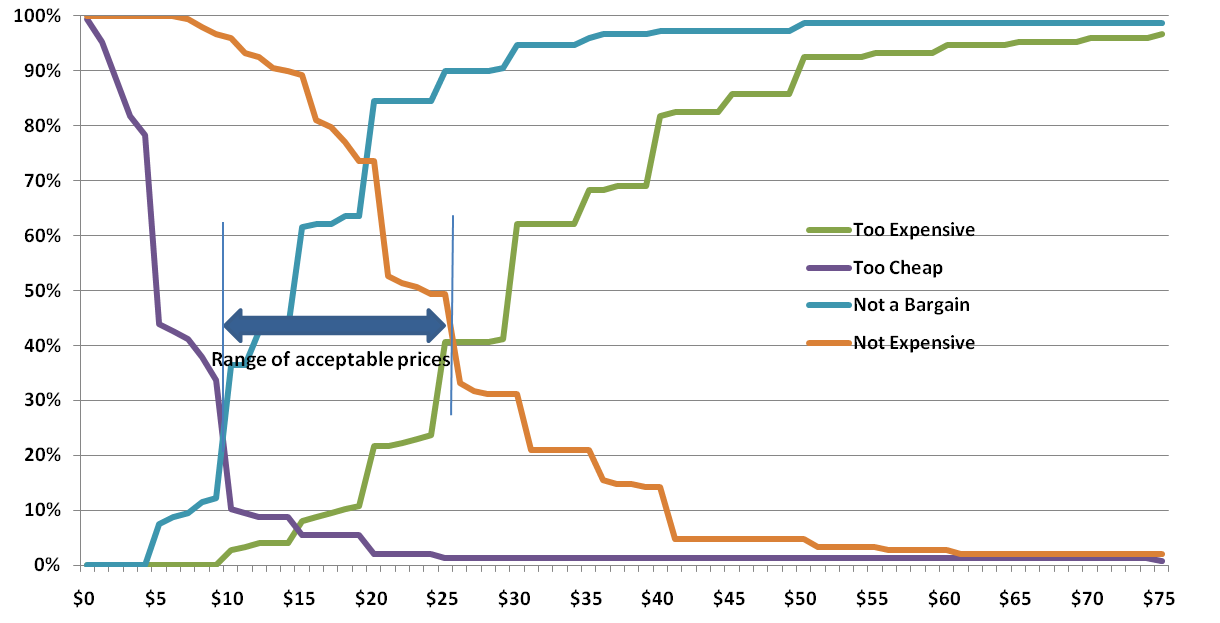
A recent article in the Seattle Times covering a poll by Elway Research gives me an opportunity to discuss statistical testing. The description of the methodology indicates, as I’d expect, that the poll was conducted properly to achieve a representative sample:
About the poll: Telephone interviews were conducted by live, professional interviewers with 405 voters selected at random from registered voters in Washington state June 9-13. Margin of sampling error is ±5% at the 95% level of confidence.
That’s a solid statement. But what struck me was that the commentary, based on the chart I’m reproducing here, might seem inconsistent with the reliability statement above.
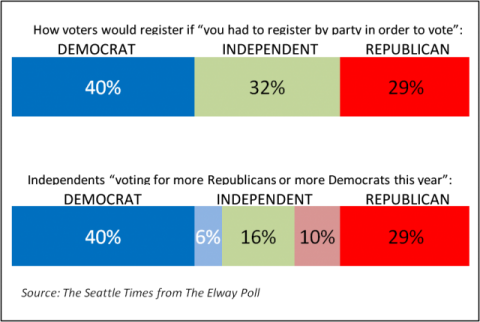
The accompanying text reads “More Washingtonians claim allegiance to Democrats than to Republicans, but independents are tilting more towards the GOP.” How can this be, when the difference is only 4% (6% more Democrats, 10% more Republicans)? The answer lies in how statistical testing works and the fact that statistical tests take into account the differences arising from different event probabilities.
First, let’s dissect the reliability statement. It means that results from this survey will be within ±5% of the true population, registered voters in this case, 19 out of 20 times if samples of this size were drawn from the registered voter list and surveyed. (One time in 20 the results could be outside of that ±5% range; that’s the result of sampling.) This ±5% range is actually the worst case and is only this high at for 50% event probabilities – meaning the situation where responses are likely to be equally split. Researchers use the worst case figure to ensure that they sample enough people for the desired reliability whatever the results are. In this case, the range for Independents leaning towards Democrats is ±2.3% (i.e. 3.7% to 8.3%) while the range for Independents leaning towards the GOP is ±2.9% (i.e. 7.9% to 12.9%). But these ranges overlap so how can the statement about tilting more to the Republicans be made with confidence?
We need to run statistical tests to apply more rigor to the reporting. In this case t-tests or z-tests will show the answer we need. The t-test is perhaps more commonly used because if works with smaller sample sizes, although we have a large enough sample here for either. Applying a t-test to the 6% and 10% results we find that the t-score is 2.02 which is greater than the 1.96 needed for 95% confidence. The differences in proportions are NOT likely due to random chance, and the statement is correct.
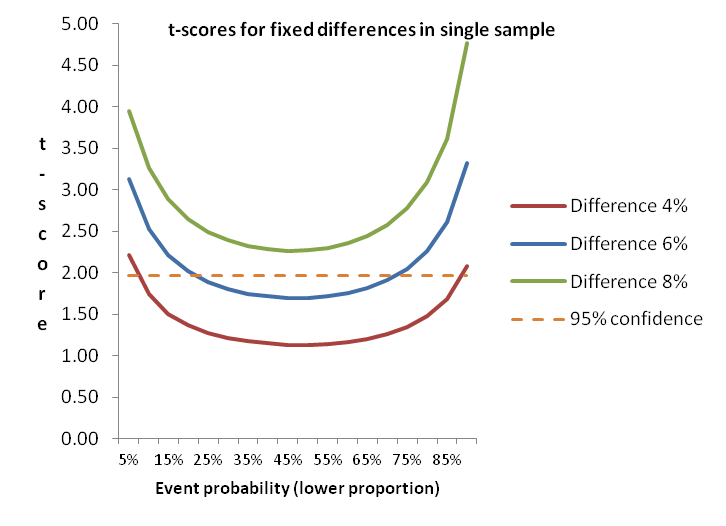
To illustrate the impact of event probability on statistical testing, this diagram shows how smaller differences in proportions are more able to discriminate differences as the event probability gets further away from the midpoint. Note that even at 6% difference results between about 20% and 70% (for the lower proportion) won’t generate a statistically significant difference, while at 8% difference the event probability doesn’t matter. Actually, 7% is sufficient – just.
Without using statistical testing, you won’t be sure that the survey results you see for small differences really mean that the groups in the surveyed population differ. How can you prioritize your efforts for feature A versus feature B if you don’t know what’s really important? Do your prospects differ in how they find information or make decisions to buy? You can create more solid insights and recommendations if you test.
Tools for statistical testing
The diagram above shows how things work, and is a rule of thumb for one type of testing. But it is generally best to use one or more tools to do significance testing.
Online survey tools don’t generally offer significance testing. The vendors tell me that users can get into trouble, and they don’t want to provide support. So you are need to find your own solutions. If you are doing analysis in Excel you can use t-tests and z-tests that are included in the Data Analysis Toolpak. But these only work on the individual results so if you are trying to look at aggregate proportions (as might be needed when using secondary research as I did above) you need a different tool. Online calculators are available from a number of websites, or you might want to download a spreadsheet tool (or build your own from the formulae). These tools are great for a quick check for a few data points without having to enter a full data set.
SPSS has plenty of tests available, so if you are planning on doing more sophisticated analysis yourself, or if you have a resource you use for advanced analysis then you’ll have the capability available. But SPSS, besides being expensive, isn’t all that efficient for large numbers of tests. I use SPSS for regressions, cluster analysis and the like, but I prefer having a set of crosstabs to be able to quickly spot differences between groups in the target population. We still outsource some of this work to specialists, but have found that most of full-service engagements include so we recently added WinCross to our toolbag. We are also making the capability available for our clients who subcontract to 5 Circles Research.
WinCross is a desktop package from The Analytical Group offering easy import from SPSS or other data formats. Output is available in Excel format, or as an RTF file for those who like a printed document (like me). With the printed output you can get up to about 25 columns in a single set (usually enough, but sometimes two sets are needed), with statistical testing across multiple combinations of columns. Excel output can handle up to 255 columns. There are all sorts of features for changing the analysis base, subtotals and more, all accessible from the GUI or by editing the job file to speed things up. It’s not the only package out there, but we like it, and the great support.
Conclusion
I hope I’ve convinced you of the power of statistical testing, and given you a glimpse of some of the tools available. Contact us if you are interested in having us produce crosstabs for your data.
Idiosyncratically,
Mike Pritchard